1554. Запрещенные строки

Строка, состоящая из букв A, B и C, называется запрещенной, если в ней встречаются три подряд буквы, одна из которых A, другая B, а третья C. Например, строка BAACAACCBAAA является запрещенной, в то время как AABBCCAABB нет.

Вычислите количество незапрещенных строк длины n.

Вход. Каждая строка содержит одно число n (1 ≤ n ≤ 30).

Выход. Для каждого значения n выведите в отдельной строке количество незапрещенных строк длины n.

Пример входа	Пример выхода
2 3 4	9 21 51

РЕШЕНИЕ

рекурсия

Анализ алгоритма

Занесем в rep[i] количество незапрещенных строк длины i, у которых две последние буквы одинаковы. В ячейке nonrep[i] будем хранить число незапрещенных строк длины i, у которых две последние буквы разные. Ответом на задачу будет значение rep[n] + nonrep[n].

Вычислим непосредственно значения ячеек:

Вычисление rep[i]. На место i - ой буквы необходимо ставить ту же букву, которая стоит на (i – 1) - ом месте.

rep[i] = rep[i – 1] + nonrep[i – 1]

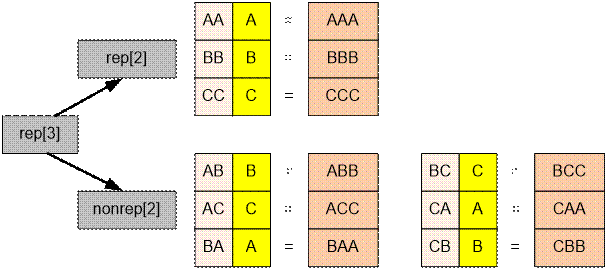
Вычисление nonrep[i]. Если (i – 1) - ая и (i – 2) - ая буквы одинаковы, то на i - ое место можно поставить любую из двух букв, не совпадающую с ней. Если (i – 1) - ая и (i – 2) - ая буквы разные, то (i – 1) - ую букву продублировать в качестве i - ой нельзя, нельзя поставить на i - ое место букву, отличную от (i – 1) - ой и (i – 2) - ой (три разные буквы подряд ставить запрещено). Поэтому в этом случае на i - ое место следует ставить (i – 2) - ую букву.

nonrep[i] = 2 * rep[i – 1] + nonrep[i – 1]

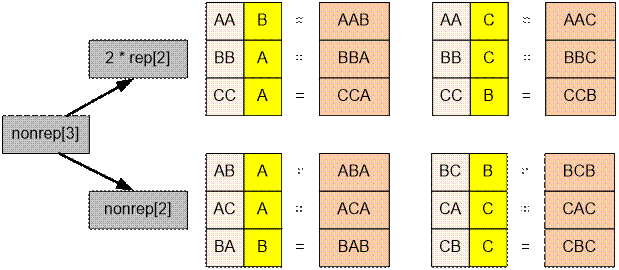
Например, ячейки массивов rep и nonrep будут содержать следующие значения:

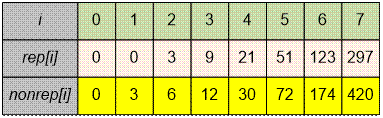
Если обозначить через rep(n) и nonrep(n) функции, вычисляющие количество незапрещенных строк длины n соответственно с повторяющимися двумя последними буквами и не повторяющимися, то можно записать рекуррентное соотношение:

,

Реализация алгоритма

Объявим глобальные переменные.

long long rep[31], nonrep[31];

Заполняем ячейки массивов rep и nonrep согласно выше приведенным формулам.

long long countNotForbidden(int n)

{

int i;

rep[1] = 0; rep[2] = 3;

nonrep[1] = 3; nonrep[2] = 6;

for(i = 3; i <= n; i++)

{

rep[i] = rep[i-1] + nonrep[i-1];

nonrep[i] = 2 * rep[i-1] + nonrep[i-1];

}

return rep[n] + nonrep[n];

}

Основная часть программы.

while(scanf("%d",&n) == 1)

{

res = countNotForbidden(n);

printf("%lld\n",res);

}

Реализация алгоритма – рекурсия с запоминанием

#include <stdio.h>

#include <string.h>

int n;

long long repMem[31], nonrepMem[31];

long long nonrep(int n);

long long rep(int n)

{

if (n == 1) return 0;

if (n == 2) return 3;

if (repMem[n] != -1) return repMem[n];

return repMem[n] = rep(n - 1) + nonrep(n - 1);

}

long long nonrep(int n)

{

if (n == 1) return 3;

if (n == 2) return 6;

if (nonrepMem[n] != -1) return nonrepMem[n];

return nonrepMem[n] = 2 * rep(n - 1) + nonrep(n - 1);

}

int main(void)

{

memset(repMem,-1,sizeof(repMem));

memset(nonrepMem,-1,sizeof(nonrepMem));

while(scanf("%d",&n) == 1)

printf("%lld\n",rep(n) + nonrep(n));

return 0;

}

Java реализация

import java.util.*;

public class Main

{

static int MAX = 31;

static long rep[] = new long[MAX], nonrep[] = new long[MAX];

static long countNotForbidden(int n)

{

rep[1] = 0; rep[2] = 3;

nonrep[1] = 3; nonrep[2] = 6;

for(int i = 3; i <= n; i++)

{

rep[i] = rep[i-1] + nonrep[i-1];

nonrep[i] = 2 * rep[i-1] + nonrep[i-1];

}

return rep[n] + nonrep[n];

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

while(con.hasNextInt())

{

int n = con.nextInt();

long res = countNotForbidden(n);

System.out.println(res);

}

}

}

Java реализация – рекурсия с запоминанием

import java.util.*;

public class Main

{

static long repMem[] = new long[31];

static long nonrepMem[] = new long[31];

static long rep(int n)

{

if (n == 1) return 0;

if (n == 2) return 3;

if (repMem[n] != -1) return repMem[n];

return repMem[n] = rep(n - 1) + nonrep(n - 1);

}

static long nonrep(int n)

{

if (n == 1) return 3;

if (n == 2) return 6;

if (nonrepMem[n] != -1) return nonrepMem[n];

return nonrepMem[n] = 2 * rep(n - 1) + nonrep(n - 1);

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

Arrays.fill(repMem, -1);

Arrays.fill(nonrepMem, -1);

while(con.hasNext())

{

int n = con.nextInt();

System.out.println(rep(n) + nonrep(n));

}

con.close();

}

}